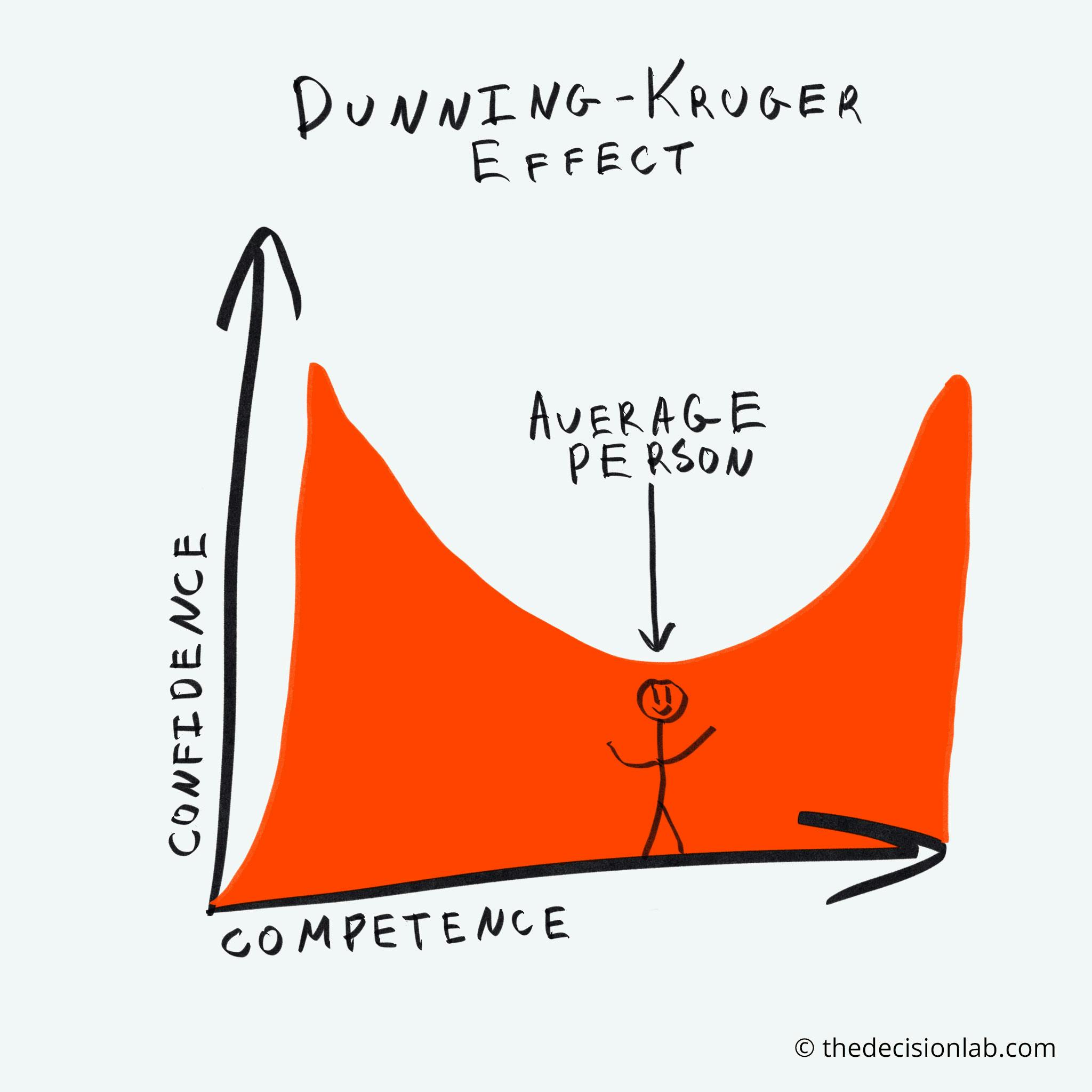
The Dunning-Kruger Effect Is a Statistical Artifact

The Dunning-Kruger effect, named after psychologists David Dunning and Justin Kruger, supposedly highlights a cognitive bias where individuals with limited knowledge or skill in a specific domain tend to overestimate their expertise in that area. This phenomenon arises due to a lack of metacognitive awareness, meaning these individuals are unable to accurately gauge their own competence. Instead, they often harbor an unwarranted confidence in their abilities, leading them to believe they are more proficient than they truly are. Conversely, individuals with genuine expertise may underestimate their competence, assuming that others find tasks as easy as they do, known as the "imposter syndrome."

This feels intuitively true. We all know arrogant fools and wise, modest, uncertain sages. Having a scientific theory/phenomenon as an "explanation" feels validating of the reality of this experience. However, the Dunning-Kruger effect is, ironically, itself an example where a modicum of knowledge in psychology and statistics has fooled many into reading deep meaning into a statistical artifact.

The statistical artifact that underlies the Dunning-Kruger effect can be demonstrated in a thought experiment. It has been demonstrated numerically a number of times, but I think it can be illustrated more simply.

Imagine we have 1,000 robots. We will have them each play two games of chance. We distribute a spinner to each of them. The spinner arcs are divided into a 'correct' and 'wrong' section. The size of the 'correct' arc of each spinner is randomly assigned, to represent a normalized distribution of 'expertise'. This will produce a normal distribution of performance on a test of knowledge. We also hand each robot a die to roll, representing each robot's self-assessment of which performance bin it fell into (rolling a one = 0-16.7%, rolling a six = 83.3-100%).

We then have the robots execute a series of one hundred spins, representing their answers to a test of knowledge. At the end, we have each robot roll a die to represent their self-assessment. Note there is no actual measurement of expertise or metacognition going on with these robots, we are simply generating equivalent statistics to the Dunning-Kruger experiments.

What happens in this experiment is the interaction of the spinner and coin flip distributions creates a skew. No robot can get less than zero or more than 100 "correct" answers. However, those robots at the top or bottom of the performance distribution will appear to under- or over-estimate their performance simply because of the cutoff at 100% and 0%, respectively!

References

An introduction to the Dunning-Kruger effect, a theory-phenomenon that "explains" a lot of things for people:

Dunning–Kruger Effect - The Decision Lab

Dunning–Kruger Effect explains why the least competent at a task often incorrectly rate themselves as high-performers because they do not know otherwise.

The Decision Lab

A takedown of the Dunning-Kruger effect:

Debunking the Dunning–Kruger effect

John Cleese, the British comedian, once summed up the idea of the Dunning–Kruger effect as, “If you are really, really stupid, then it’s impossible for you to know you are really, really stupid.” A quick search of the news brings up dozens of headlines connecting the Dunning–Kruger effect to everything from work to empathy and even to why Donald Trump was elected president.

Phys.orgEric C. Gaze

A numerical simulation from the above debunker from which our simplified robot thought experiment is derived:

Random Number Simulations Reveal How Random Noise Affects the Measurements and Graphical Portrayals of Self-Assessed Competency

Self-assessment measures of competency are blends of an authentic self-assessment signal that researchers seek to measure and random disorder or “noise” that accompanies that signal. In this study, we use random number simulations to explore how random noise affects critical aspects of self-assessment investigations: reliability, correlation, critical sample size, and the graphical representations of self-assessment data. We show that graphical conventions common in the self-assessment literature introduce artifacts that invite misinterpretation. Troublesome conventions include: (y minus x) vs. (x) scatterplots; (y minus x) vs. (x) column graphs aggregated as quantiles; line charts that display data aggregated as quantiles; and some histograms. Graphical conventions that generate minimal artifacts include scatterplots with a best-fit line that depict (y) vs. (x) measures (self-assessed competence vs. measured competence) plotted by individual participant scores, and (y) vs. (x) scatterplots of collective average measures of all participants plotted item-by-item. This last graphic convention attenuates noise and improves the definition of the signal. To provide relevant comparisons across varied graphical conventions, we use a single dataset derived from paired measures of 1154 participants’ self-assessed competence and demonstrated competence in science literacy. Our results show that different numerical approaches employed in investigating and describing self-assessment accuracy are not equally valid. By modeling this dataset with random numbers, we show how recognizing the varied expressions of randomness in self-assessment data can improve the validity of numeracy-based descriptions of self-assessment.

Digital Commons @ University of South FloridaEdward Nuhfer